linear data structure-

 

Data structure-

  1)linear data structure

       i)  array

      ii)  link list

      iii) stack

      iv) queue

  2)non linear data structure

         i) tree

         ii) graph

link list;-

link list is linear data structure ,which are connected to link. thr  elements are not stored at contiguous memory locations. 

types of link list-

1.singly link list

2.doubly link list

3.singly circular link list

4.doubly circular link list

 operations on singly link  list & doubly link list:

 1)creatlist

2) display

3)sorting

4)searching

5)insertion -       

     i)insert at begin

     ii)insert at last

     iii)insert at any position

6)deletion-        

     i)delete from begin

     ii)delete from last

     iii)delete from any position

     iv)delete by value

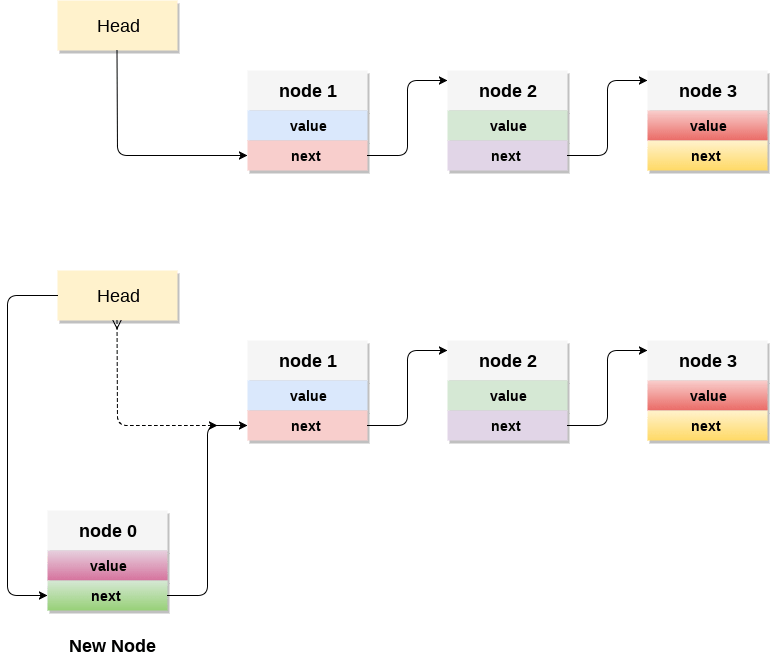
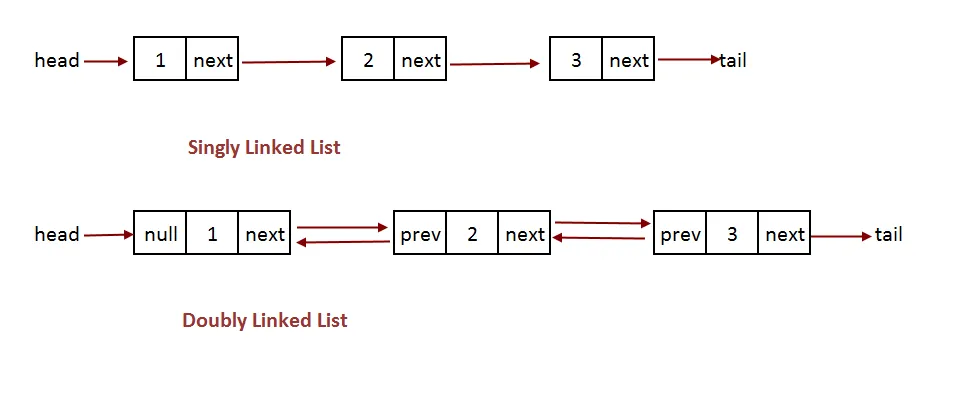
1]Basic structure of a singly linked list

     struct node {

int data; // Data struct node * next; // Address };

2]Basic structure of a doubly linked list

struct node {

int data; // Data  

struct node * next,*prev; // Address

};

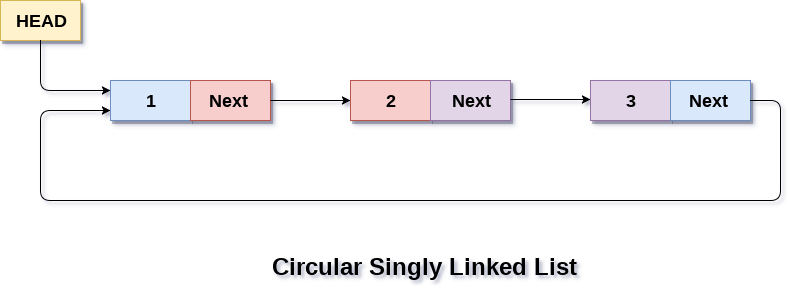
3]Circular Singly Linked List

In a circular Singly linked list, the last node of the list contains a pointer to the first node of the list. We can have circular singly linked list as well as circular doubly linked list.

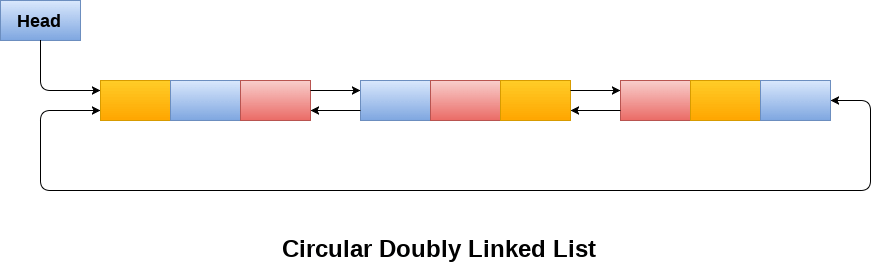
Circular Doubly Linked List

Circular doubly linked list is a more complexed type of data structure in which a node contain pointers to its previous node as well as the next node. Circular doubly linked list doesn't contain NULL in any of the node. The last node of the list contains the address of the first node of the list. The first node of the list also contain address of the last node in its previous pointer.

                            STACK

STACK-

                 stack is linear data structure,which is performed LIFO (last in first out ) manner.

 Types of stack -

                   1)static implementation of stack

                   2)dynamic implementation stack

Array implementation of Stack

In array implementation, the stack is formed by using the array. All the operations regarding the stack are performed using arrays.

The following are some common operations implemented on the stack:

• push(): When we insert an element in a stack then the operation is known as a push. If the stack is full then the overflow condition occurs.
• pop(): When we delete an element from the stack, the operation is known as a pop. If the stack is empty means that no element exists in the stack, this state is known as an underflow state.
• isEmpty(): It determines whether the stack is empty or not.
• isFull(): It determines whether the stack is full or not.
• peek(): It returns the element at the given position.
• display(): It prints all the elements available in the stack.

      push opearation:

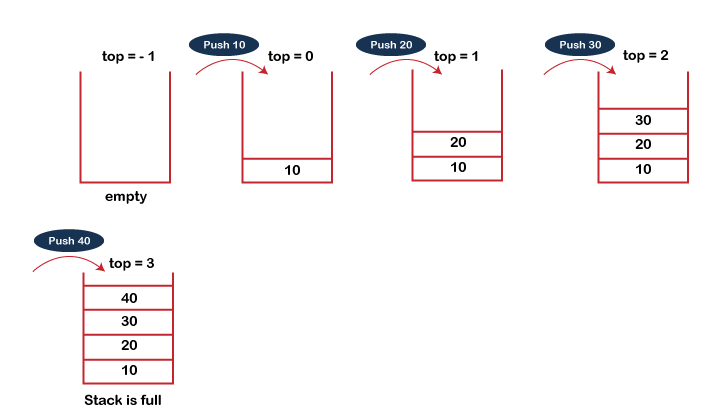
The steps involved in the PUSH operation is given below:

• Before inserting an element in a stack, we check whether the stack is full.
• If we try to insert the element in a stack, and the stack is full, then the overflow condition occurs.
• When we initialize a stack, we set the value of top as -1 to check that the stack is empty.
• When the new element is pushed in a stack, first, the value of the top gets incremented, i.e., top=top+1, and the element will be placed at the new position of the top.
• The elements will be inserted until we reach the max size of the stack.

algorithm:

1. begin   
2.     if top = = size - 1 then stack is full   
3.     top = top + 1  
4.     stack (top) : = item;  
5. end   

pop opearation:

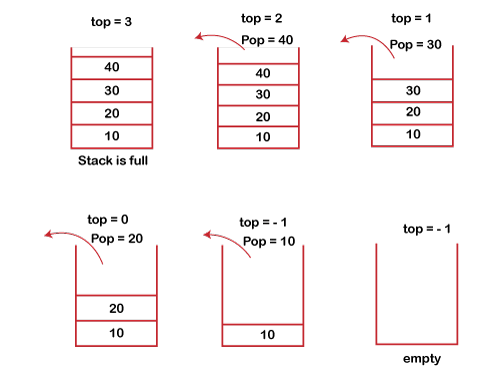
The steps involved in the POP operation is given below:

• Before deleting the element from the stack, we check whether the stack is empty.
• If we try to delete the element from the empty stack, then the underflow condition occurs.
• If the stack is not empty, we first access the element which is pointed by the top
• Once the pop operation is performed, the top is decremented by 1, i.e., top=top-1.

algorithm:

1. begin   
2.     if top = = -1 then stack is empty;   
3.     item = stack(top);  
4.     top = top - 1;  
5. end;    

peek opearation:

1. Begin   
2.     if top == -1 then stack is empty    
3.     item = stack[top]   
4.     return item  
5. End    

display opearation:

1. Begin   
2.     if top == -1 then stack empty    
3.     i = top
4.    if(i>=0)  then,
5.     print stack[i]
6.     i--
7. End    

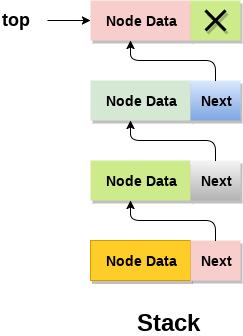
Dynamic  implementation of Stack-

In linked list implementation of stack, the nodes are maintained non-contiguously in the memory. Each node contains a pointer to its immediate successor node in the stack. Stack is said to be overflown if the space left in the memory heap is not enough to create a node.

structure of dynamic stack

  typedef struct node {

int data; // Data struct node * next; // Address }STACK;

Algorithms-

firstly top=NULL;

push operation-

1.make newnode

2.newnode->data=num

3.newnode->next=top

4.top=newnode.

pop operation-

1. temp=top

2. if top==null then, stack is empty

3. else print top->data,

top=top->next

free(temp)

peek operation-

1. if top==null then, stack is empty

2. else print top->data

display opearation-

1. temp=top

2. if top==null then, stack is empty

3. else if temp!=null then

print temp->data

temp=temp->next

                              

                    QUEUE

QUEUE-

                  Queue is  linear data structure,which is performed FIFO (first in first out ) manner.

 

Types of queue-

                      1)Static implementation of queue

                      2)Dynamic implementation queue

Queue

1. A queue can be defined as an ordered list which enables insert operations to be performed at one end called REAR and delete operations to be performed at another end called FRONT.

2. Queue is referred to be as First In First Out list.

3. For example, people waiting in line for a rail ticket form a queue.

Types of Queue

There are four different types of queue that are listed as follows -

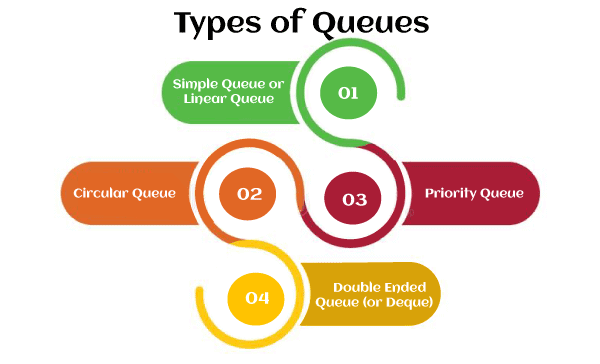
• Simple Queue or Linear Queue
• Circular Queue
• Priority Queue
• Double Ended Queue (or Deque)

Array representation of Queue

We can easily represent queue by using linear arrays. There are two variables i.e. front and rear, that are implemented in the case of every queue. Front and rear variables point to the position from where insertions and deletions are performed in a queue. Initially, the value of front and queue is -1 which represents an empty queue. Array representation of a queue containing 5 elements along with the respective values of front and rear, is shown in the following figure.

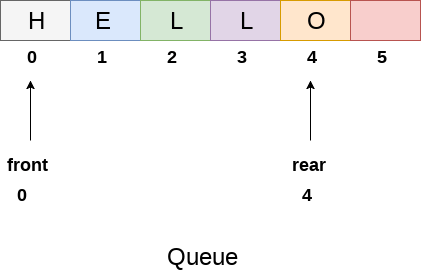
The above figure shows the queue of characters forming the English word "HELLO". Since, No deletion is performed in the queue till now, therefore the value of front remains -1 . However, the value of rear increases by one every time an insertion is performed in the queue. After inserting an element into the queue shown in the above figure, the queue will look something like following. The value of rear will become 5 while the value of front remains same.

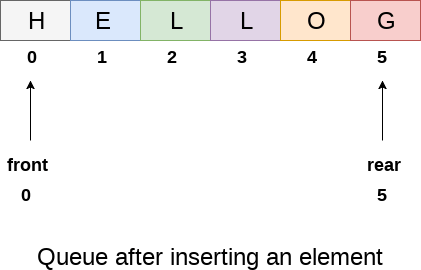
After deleting an element, the value of front will increase from -1 to 0. however, the queue will look something like following.

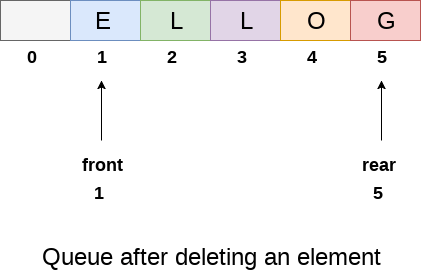
Algorithm to insert any element in a queue

Check if the queue is already full by comparing rear to max - 1. if so, then return an overflow error.

If the item is to be inserted as the first element in the list, in that case set the value of front and rear to 0 and insert the element at the rear end.

Otherwise keep increasing the value of rear and insert each element one by one having rear as the index.

 

Algorithm

• Step 1: IF REAR = = MAX - 1
  Write QUEUE IS OVERFLOW
  Go to step
  [END OF IF]
• Step 2: IF FRONT = = -1 and REAR = = -1
  SET FRONT = REAR = 0
  ELSE
  SET REAR = REAR + 1
  [END OF IF]
• Step 3: Set QUEUE[REAR] = NUM
• Step 4: EXIT

Algorithm to delete an element from the queue

If, the value of front is -1 or value of front is greater than rear , write an underflow message and exit.

Otherwise, keep increasing the value of front and return the item stored at the front end of the queue at each time.

Algorithm

• Step 1: IF FRONT = -1 or FRONT > REAR
  Write UNDERFLOW
  ELSE
  SET VAL = QUEUE[FRONT]
  SET FRONT = FRONT + 1
  [END OF IF]
• Step 2: EXIT

Algorithm Of display function-

        1.SET TOP = FRONT

       2.IF TOP == -1 && FRONT == -1

                 THEN WRITE QUEUE IS EMPTY

       3.ELSE WHILE(TOP <= FRONT)

                THEN PRINT QUEUE[TOP]

                       TOP++

Algorithm Of Peek function-

    

       1.IF TOP == -1 && FRONT == -1

                 THEN WRITE QUEUE IS EMPTY

        2.ELSE  WRITE FRONT OF QUEUE 

                        QUEUE[FRONT]

Drawback of array implementation

Although, the technique of creating a queue is easy, but there are some drawbacks of using this technique to implement a queue.

• Memory wastage : The space of the array, which is used to store queue elements, can never be reused to store the elements of that queue because the elements can only be inserted at front end and the value of front might be so high so that, all the space before that, can never be filled.

Dynamic representation of Queue-

  In a linked queue, each node of the queue consists of two parts i.e. data part and the link part. Each element of the queue points to its immediate next element in the memory.

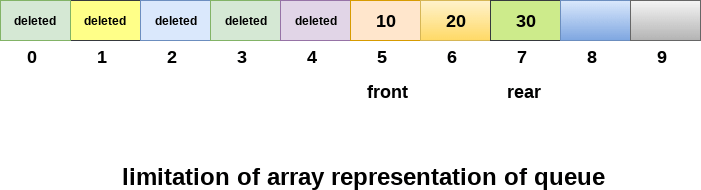
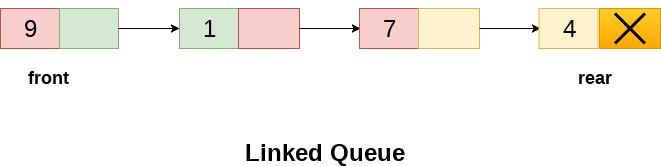
In the linked queue, there are two pointers maintained in the memory i.e. front pointer and rear pointer. The front pointer contains the address of the starting element of the queue while the rear pointer contains the address of the last element of the queue.

Insertion and deletions are performed at rear and front end respectively. If front and rear both are NULL, it indicates that the queue is empty.

The linked representation of queue is shown in the following figure.

opearation on queue-

firstly front=0 and rear=0

  ENQUEUE OPEARATION-

1.CREATE newnode

2.newnode->data=num

3.newnode->next=NULL

4.IF FRONT==0 && REAR==0

THEN FRONT=REAR=newnode

5. rear->next=newnode

6. rear=newnode

  DEQUEUE OPEARATION-

  1.temp=front

2.IF FRONT==0 && REAR==0

THEN WRITE QUEUE IS EMPTY

3.ELSE POP ELEMENT=FRONT->DATA

4.FRONT=FRONT->NEXT

5.FREE(temp)

 

   PEEK OPEARATION-

           1.IF FRONT==0 && REAR==0

THEN WRITE QUEUE IS EMPTY

2.PRINT FRONT ELEMENT = FRONT->DATA

   DISPLAY OPEARATION-

           1.IF FRONT==0 && REAR==0

THEN WRITE QUEUE IS EMPTY

2.TEMP=FRONT

3.ELSE WHILE TEMP!=NULL

PRINT TEMP->DATA

TEMP=TEMP->DATA